Uit de vorige hoofdstukken zou men kunnen besluiten dat er zoiets bestaat als een ordenend algoritme. Het is mogelijk dat u hier een soort van theologische figuur inziet, maar daar ga ik liever niet op in. Het resultaat van dit ordenende algoritme is alles wat u rondom u kan waarnemen. Alle materie, levend of dood, werd ooit door dit ordenende algoritme verenigd tot de vormen die ze nu aanneemt. Het is enkel jammer dat ik dit algoritme niet even gauw op papier kan zetten. Ik kan wel aan de hand van een klein voorbeeld de eventuele werking van zo een algoritme illustreren. In het dit hoofdstuk leg ik u uit hoe men aan de hand van enkele eenvoudige regels al kan komen tot een veelheid aan vormen. Een aselecte creatie van vormen waaruit men later als vormgever eventueel een seclectie kan maken (merk op de Darwin Two-Step in een ander kleedje).

Ik heb twee werelden uitvoerig besproken in de vorige hoofdstukken, één wereld was het universum en de andere wereld waren onze hersenen. In de twee werelden was er eerst een chaos waarna deze werd omgevormd tot orde. In het universum kwamen de oerkrachten tot rust in kristalroosters, moleculen, kettingreacties, evenwichts­reacties, organismen, hemellichamen ... In onze hersenen vormden zich uit de wirwar van elektro-chemische-prikkels, gedachten, structuren, ideeën ... In mijn simulatie gebruik ik een rooster van 60 cellen waarop willekeurig énen en nullen worden geplaatst. Voor technische redenen die ik u wil besparen gebruik ik hiervan 52 cellen zoals aangegeven in onderstaande figuur:

Het aantal mogelijke kombinaties om zo een rooster op te vullen met énen en nullen is 2⁵² dat zijn ongeveer 4 500 000 000 000 000 mogelijkheden. Het spreekt dus van zelf dat de willekeurige keuze die ik maak vrij aselct is. In dit stadium maak ik dus een kunstmatige kleine chaos, u moet het zich voorstellen als een plaats waar slechts 52 dingen zijn ontstaan na de oerknal die deze plaats heeft doen ontstaan. In ons universum zijn er veel meer dingen ontstaan, maar daarom is dit ook maar een simulatie. We hebben dus een ontstaans-chaos van 52 deeltjes. Hoe gaan deze deeltjes op elkaar reageren? Welke vormen of patronen gaan er ontstaan? Gaan ze wel reageren?

Om zulke fenomenen te onderzoeken maakt men in de wetenschap gebruik van cellulaire automaten. Een duur woord voor een computersimulatie die men gemakkelijk kan doen met een schrift met ruitjespapier. Op het eerste blad bakenen we een gebied af, laten we zeggen 4x4 ruitjes. We bevinden ons op pagina 1 en geven dit blad overeenkomstig de titel tijdstip 1 of uitgangssituatie. We zetten willekeurig enkele punten in het rooster. Bijvoorbeeld zo

Dit rooster bevat veel informatie : we kennen het tijdstip (T1), we kennen het aantal actieve cellen (5) en we kennen de positie van deze actieve cellen (A1,B1,B2,C3,D4). Op het tweede blad van het schrift zetten we als titel tijdstip 2 en we tekenen op dezelfde plaats weer het rooster. Nu mogen we echter niet meer willekeurig punten zetten want tijdstip 2 staat in verband met tijdstip 1. We moeten regels bedenken om de overgang van T1 naar T2 mogelijk te maken. Eens dat deze regels bepaald zijn kunnen we het hele schrift vol schrijven en zien we de evolutie van de beginsituatie doorheen de tijd.

Stel dat wij een geheel van regels zouden opstellen waaraan deze 52 deeltjes zich moeten houden, wat zou er dan gebeuren? Iedereen kan wel een regel bedenken om los te laten op deze beginsituatie, maar wat is de relevantie dan van die regel ten opzichte van het ontstaan van de cosmos of van het leven? Ik heb gekozen om de regels van “the game of life” van J. H. Conway over te nemen. Het zijn slechts drie regels die de aspecten van het leven omschrijven namelijk geboorte, overleving en dood.

Indien we nu deze drie aspecten in regels gieten dan komen we op het volgende algorime uit:

• Men mag in een lege cel (een cel die een 0 bevat) een 1 plaatsen indien er in de omgeving (dit zijn de acht cellen rondom hem) exact drie cellen zijn die een 1 bevatten. Dit is de regel voor de geboorte van een 1.
• Een 1 mag blijven staan indien er in zijn omgeving twee of drie cellen een 1 bevatten. Dit is de regel van de overleving van de 1.
• De 1 die in een cel staat waar er in de omgeving minder dan twee of meer dan drie énen staan, wordt vervangen door een 0. Dit is de regel voor de dood van een 1.

Een cel kan bezet zijn of niet, in de voorstelling hiervan maakt het niets uit of er nu een bolletje staat of een 1. Ik heb moeten werken met énen omdat ik hier dan later wiskundige bewerkingen op kon uitvoeren.

We krijgen dus de volgende beginsituatie :

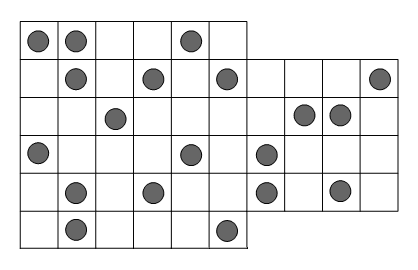
Stelt u zich voor dat dit een soort dambord is en dat de cirkels damstenen voorstellen. We plaatsen nu een gelijkaardig dambord onder dit en we passen de regels van “the game of life” toe. Zolang we geen stabiele situatie bekomen blijven we dit herhalen. Met stabiel bedoel ik dat de op elkaar volgende damborden dezelfde verdeling vertonen. U zou iets gelijkaardigs moeten krijgen :

Nu gaan we voorzichtig de damborden verwijderen en we zorgen ervoor dat de damstenen op hun plaats blijven liggen.

Ons uitgangspunt was een rooster met een willekeurige bezetting. We zijn reeds gekomen tot hetzelfde rooster maar met bepaalde hoogtes. Door het algoritme van Conway toe te passen en de geschiedenis van het rooster te onthouden zijn we gekomen tot een extra dimentie : een hoogte. Elke cel van het rooster is nu niet meer bezet of onbezet, maar bevat een waarde die weergeeft hoe dikwijls deze cel bezet is geweest in de levensduur van het rooster. We moeten slechts het aantal damstenen tellen en opschrijven in de cel. Het volgende rooster zou een uitkomst kunnen zijn.

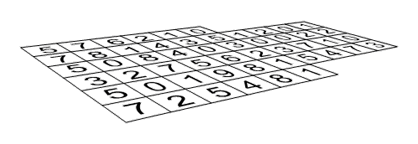
Mits wat hertekenen kunnen we tot de volgende figuur komen :

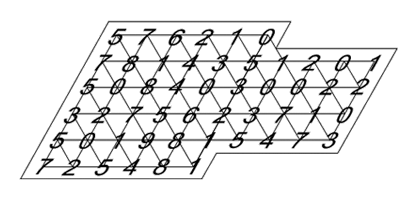
We zijn vertrokken van een willekeurige (aselecte) beginsituatie, één uit 4 500 000 000 000 000. En we zijn via een ordenend algoritme, waar slechts drie regels in zitten gekomen tot een rooster van waarden die quasi niet te voorspellen waren bij de aanvang.

Het vergt wat inbeeldingsvermogen om van dit rooster over te gaan naar een drie-dimenionele vorm, maar aan de hand van enkele schetsen lukt het wel. De vreemde vorm van dit rooster heb ik niet zomaar gekozen, het is de ontvouwing van een tetraëder (een viervlak). Indien de tetraëder wordt toegevouwen dat staan er getallen op

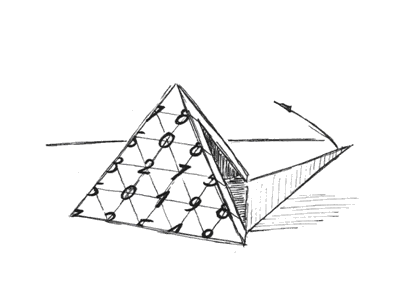
U moet zich, net zoals dat gaat bij een bol, een middelpunt voorstellen in deze tetraëder.

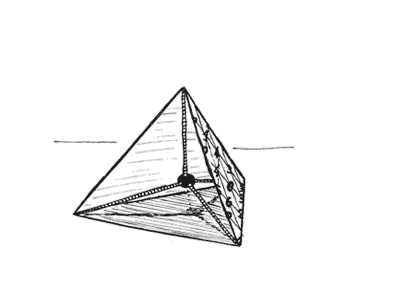
Overeenkomstig de waarden moet men nu stokjes steken door de kruisingen op de mantel van de tetraëder en in het middelpunt. De eindpunten van deze stokjes zullen achteraf de vorm van het object bepalen.

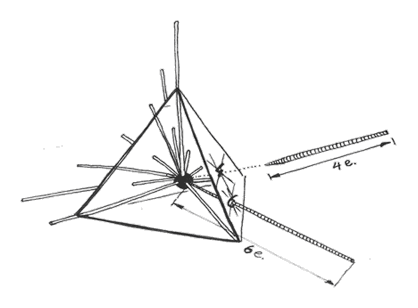
Indien u de eindpunten van de stokjes verbindt met elkaar op dezelfde manier als dat de lijnen lopen op de tetraëder, dan bekomen we de ruwe vorm van het object. Mits enkele afrondingen kunnen we tot de uiteindelijke vormen komen :

Top